Dinamicko programiranje (dp) je
princip kojim se resavaju mnogi problemi. Znaci nije kao npr. teorija grafova, gde imamo skup algoritama koji se odnose konkretno na grafove, vec je dp sam princip (stavise, mnogi se algoritmi recimo bas u teoriji grafova i oslanjaju na dinamicko programiranje). Dp se primenjuje u problemima koji imaju
optimalnu podstrukturu. To znaci, ako treba resiti neki problem za n, mi cemo resiti probleme za 1, 2, ..., n-1, i, konacno, za n. Naravno ovo ne pali uvek, pa je zato i potrebno da problem ima gore pomenutu optimalnu podstrukturu. Uglavnom su to problemi gde se trazi neko
optimalno resenje, dakle, nesto maksimalno ili minimalno. Dp neodoljivo podseca (a i jeste) na matematicku indukciju. Uzmimo banalan primer: treba naci najveci od n elemenata. Mi cemo naci najveci od 1 elementa (to je on sam). Kad imamo najveci od prvih k elemenata, nacicemo najveci od prvih k+1, tako sto cemo k+1-vi element uporediti sa dosadasnjim najvecim (od prvih k), pa ako je veci, uzimamo njega, ako ne, uzimamo onaj koji je bio najveci od prvih k. Na taj nacin cemo dobiti i najveci od svih n.
Kao sto rekoh, mnogi se algoritmi oslanjaju na dinamicko programiranje. Zato cu ja ovde navesti samo nekoliko njih, koji se ne mogu svrstati u ostalea kategorije koje cu opisati (namely, grafovski i geometrijski algoritmi).
Problem ranca
Problem ranca (knapsack problem) je verovatno najpoznatiji primer dinamickog programiranja. Postoji puno varijacija na temu ovog problema, a ja cu ovde navesti onu koju (bar ja) smatram za osnovnu. Imamo ranac u koji moze stati N zapreminskih jedinica. Imamo M predmeta, od koji svaki ima svoju zapreminu (Z) i vrednost (V). Treba naci optimalno popunjivanje ranca. Vec na prvi pogled je jasno da grabljivi (greedy) algoritam ovde ne pali. Ne mozemo uzimati predmete sa sto manjom zapreminom, jer je moguce da neki od njih imaju isuvise malu vrednost, pa nam se ne isplati. Isto tako ne mozemo uzimati ni predmete sto vece vrednosti, jer mogu imati isuvise veliku zapreminu. Ono sto moze da nam se ucini na prvi pogled, to je da treba uzimati elementa ciji je odnos vrednost/zapremina sto veci. Ali, ni ovo nije tacno! Uzmimo primer: imamo ranac velicine 8, i tri predmeta: jedan zapremine 6 i vrednosti 7, i dva zapremine po 4 i vrednosti po 4. Najveci odnos vrednost/zapremina ima prvi predmet, ali ako uzmemo njega, ne mozemo staviti vise ni jedan predmet u ranac, pa ce ukupna vrednost biti 7. Sa druge strane, uzmemo li druga dva predmeta, imacemo vrednost 8! Zato pribegavamo dinamickom programiranju. Moramo utvrditi optimalnu podstrukturu problema. Punimo rance velicina 1, 2, ..., N redom. Ako smo optimalno popunili ranac velicine k, a poslednji stavljen element je recimo i-ti, onda je jasno da izabrani predmeti (bez i-tog) optimalno popunavaju ranac velicine
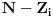
. Ovo je dovoljno da zakljucimo optimalnu podstrukturu! Ostaje jos samo da imamo neku "bazu indukcije", a to je ranac velicine 0, koji je optimalno popunjen kada u njemu nema nijednog predmeta (a i ne moze biti). Dakle, algoritam se svodi na to da idemo od 1 do N, i za svako i prodjemo brojacem j sve predmete, i proverimo da li je popunjavanje ranca velicine
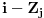
zajedno sa j-tim elementom bolje od trenutnog najboljeg popunjavanja ranca velicine i, tj. da li je
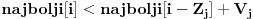
. Ako jeste, updateujemo tu vrednost. Tako cemo dobiti i optimalno popunjavanje ranca velicine N. Slozenost je ocigledno
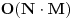
.
http://www.cs.toronto.edu/~heap/270F02/node62.html
Najduzi zajednicki podniz
Najduzi zejdnicki podniz (longest common subsequence) je problem u kome za dva niza treba odrediti najduzi koji je oboma podniz (elementi ne moraju biti uzastopni da bi cinili podniz, jedino je bitan redosled u kome se javljaju). Neka je prvi niz duzine n, drugi duzine m. Pravimo matricu best [i, j], koja predstavlja duzinu najduzeg podniza za prvih i clanova prvog niza, i prvih j clanova drugog niza. best [0, i] i best [i, 0] je 0 za svako i. Best [i, j] je best [i-1, j-1] + 1, ako su i-ti clan prvog i j-ti clan drugog niza jednaki, ili max (best [i-1, j], best [i, j-1]) ako su razliciti, za svako i od 1 do n i svako j od 1 do m. Best [n, m] je resenje problema. Primetimo da za best ne moramo koristiti matricu, jer u svakoj iteraciji koristimo samo prethodni i trenutni red te matrice, pa je dovoljno pamtiti samo 2 reda. Medjutim, ukoliko nam se trazi ne samo duzina najduzeg zajednickog podniza, vec i sam podniz, neophodno je pamtiti matricu, kako bismo mogli da rekonstruisemo "put" kroz matricu i sam niz. Slozenost algoritma je
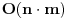
.
http://www.cs.pitt.edu/~kirk/cs1510/notes/dynnotes/node3.html
http://ranger.uta.edu/~cook/aa/lectures/applets/lcs/lcs.html
http://www.cs.fsu.edu/~cop4531/slideshow/chapter16/16-3.html
Najduzi rastuci podniz
Najduzi rastuci podniz (longest increasing subsequence) trazi najduzi rastuci rastuci podniz za dati niz, pri cemu podniz definisemo kao u prethodnom problemu. Ovo je (bar po meni) jedan od najlepsih problema koji se resavaju dinamicki. Za pocetak, primetimo da ovaj problem mozemo resiti tako sto cemo naci najduzi zajednicki podniz za dati niz i rastuce sortirani niz, sto bi vodilo slozenosti
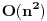
. Ali, mi hocemo bolje od ovoga. Pocecemo sa kraja niza i ici unazad (sto cesto pali kod dinamickog). Za svaki broj x, pamtimo vrednost best [x], koja predstavlja najveci broj koji je prvi u rastucem nizu duzine x. Primer, imamo niz: 3 6 4 9 8 10. Polazimo od 10 i idemo u nazad. Kad razmatramo recimo broj 4, best [2] je 9 (sto predstavlja podniz 9 10). Ovde se i krije optimalna podstruktura problema, jer, sigurno nam je bolje da uzmemo niz 9 10 i na njegov pocetak kalemimo elemente, nego na niz 8 10. Tako iduci ulevo, mozemo da "nakalemimo" pocetke niza, i updateujemo best vrednosti ako je potrebno. Jasno, po zavrsetku ce najveci index u best nizu koji je razlicit za koji smo nasli neku vrednost biti resenje. Slozenost ovog algoritma bi bila
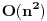
, jer za svaki element moramo proci ceo best niz. Naravno, cim dodjemo do nekog indexa u best nizu za koji nemamo upisano nista (dakle ne postoji rastuci podniz te duzine od dosad prodjenih elemenata), ne moramo nastavljati dalje, jer sigurno ne postoje ni duzi podnizovi, pa ce algoritam u sustini raditi i dosta brze u praksi. Medjutim, postoji cak i poboljsanje! Primetimo da je best niz sortiran! Zato, umesto linearne, mozemo koristiti binarnu pretragu da svakom elementu pronadjemo "mesto" u best nizu. Slozenost je onda
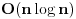
. Primetimo jos i da opisanim algoritmom mozemo samo naci duzinu podniza, a ne i sam podniz. Kao odlican reference o ovom problemu, prilazem u attachmentu text sa
www.usaco.org.
O dinamickom programiranju nemam jos mnogo stosta reci (algorithm-wise), jer je to, kao sto sam vec rekao, princip resavanja problema. Za dalji reference obratite se navedenim linkovima, a ako postoji interesovanje, mozda napisem posebnu temu posvecenu dinamickom programiranju. Obavezna literatura za ovu oblast je knjiga "Dinamicko programiranje" Milana Vugdelije.
http://mat.gsia.cmu.edu/classes/dynamic/dynamic.html
[Ovu poruku je menjao IsrkiboyI dana 15.05.2005. u 04:50 GMT+1]
I HAD A NIGHTMARE
IT ALL STARTED NORMAL
10101010
10110011
THEN ALL OF A SUDDEN
1100102
GAAAAH
_____________________________
www.princeton.edu/~skrstic
www.niwifi.co.sr